ZADANIE D - Siatka trójkątna

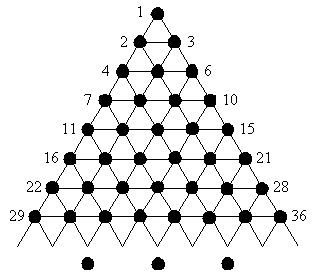
Niech będzie dana następująca siatka trójkątna o nieskończonym rozmiarze złożona z punktów i krawędzi:

Punkty w siatce można ponumerować od strony lewej do prawej i od góry do dołu. Zbiory pewnych punktów siatki tworzą figury geometryczne. Przykładowo zbiory punktów {1, 2, 3} i {8, 10, 19} tworzą trójkąty. Zbiory punktów {11, 13, 26, 24} i {2, 7, 9, 18} tworzą z kolei równoległoboki. Natomiast zbiory punktów {4, 5, 9, 13, 12, 7} i {8, 10, 17, 21, 32, 34} tworzą sześciokąty.

Twoim zadaniem jest napisanie programu, który dla zadanego zbioru punktów sprawdzi czy tworzą one jedną z figur: trójkąt, równoległobok lub sześciokąt. Punkty tworzą figurę jeżeli spełnione są następujące warunki:

• wierzchołki figury pokrywają się z punktami siatki,
• krawędzie figury pokrywają się z krawędziami siatki,
• wszystkie krawędzie figury mają taką samą długość.

Dane wejściowe:

W pierwszym wierszu znajduje się liczba M, będąca liczbą zestawów danych wejściowych.

Pierwszy wiersz zestawu danych wejściowych zawiera liczbę N (N = 3, 4 lub 6) będącą liczbą punktów. Kolejny wiersz zawiera N liczb całkowitych K (1 ≤ K ≤ 180.300) będących punktami siatki.

Dane wyjściowe:

Dane wyjściowe składają się z M wierszy. Jeden wiersz odpowiada jednemu zestawowi danych i zawiera cyfrę "1", jeżeli zbiór punktów tworzy figurę zgodnie z zasadami opisanymi w treści zadania, lub cyfrę "0" w przeciwnym przypadku.

Przykładowe dane wejściowe:

8
4
3 3 3 3
3
14 32 35
4
11 13 29 31
4
26 11 13 24
6
4 5 9 13 12 7
6
1 2 3 4 5 6
4
11 13 23 25
3
1 12 14
	

Przykładowe dane wyjściowe:

0
1
0
1
1
0
0
0