Gaston

Gaston is an employee of a famous comic magazine. One of his tasks (the one he dislikes most) is archiving mail. He archives infrequently, so a large part of his desk is taken up by an enormous pile of unprocessed letters. Sometimes, one of the editors needs a particular letter and Gaston is faced with the problem of finding that letter in the pile.

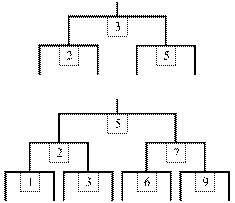
Gaston realizes that he has a retrieval problem. Using sticks and threads, he has designed a system for better retrieving unarchived letters. In the middle of a stick, he attaches a letter. At both ends of the stick, a thread is attached where another stick (with letter and threads) can be fastened. He arranges the letters such that all letters under the left thread of a stick are alphabetically before the letter in the middle and the letters under the right thread are alphabetically after the letter in the middle. As this is true for every stick, this system creates a sorted tree, in which it is easy to find letters.

When making a prototype, Gaston found out that he has a balancing problem. If there is a difference in weight between the ends of a stick, the stick is unbalanced, and the whole system collapses in an even bigger mess than before. Using some extra thread, Gaston invented an asymmetric fix in which a stick is still balanced if the left side contains one more letter than the right side. If the right side contains more letters, the stick is always unbalanced, so the fix is indeed asymmetric.

Opinions about Gaston differ. He believes that he is a genius, but others are not so certain. The editors point out that when a letter is added, there is a fair chance that the tree gets out of balance and must be rearranged. We want you to find out how often the tree (or a subtree) must be rearranged, given a tree and a sequence of incoming letters.

We have simplified the problem a bit. All letters have the same weight. Every letter has a unique (positive) number. The letters must be arranged according to their number. A stick is balanced if the left side contains the same number of letters as the right side or at most one more.

A letter is added according to the following procedure: if its number is lower than the number of the letter on the stick, it is added to the left thread. If its number is higher, it is added to the right thread. Following this procedure repeatedly, eventually a free thread is found. The letter is then attached to a fresh stick (having a free thread on both ends) which is tied to the free thread. Then, starting at the top, working downwards, the balance of all sticks are checked. If a stick is unbalanced, a balancing step is executed. Because a balancing step might cause other sticks to become unbalanced, the whole tree is checked again from top to bottom for unbalanced sticks. This is repeated until no unbalanced sticks are found.

A balancing step is defined as bringing one unbalanced stick s into balance by removing a letter from the heavy side of the stick and adding one to the light side. This is done according to the following procedure:

1. remove the letter l_old from the stick s

2. find an appropriate letter l_new from the heavy side and attach it to the stick s

3. add l_old on the other side of s.

A balancing step can result in more sticks being unbalanced! Because l_new is removed from it's old position, an unbalanced stick can be left behind. Also, adding the former letter can result in a new unbalanced stick. Getting these sticks balanced again is not a part of this balancing step(!); they are done in future balancing steps. Note that each balancing step must be done carefully in order to ensure that the tree remains sorted.

The problem is to find out how many balancing steps are needed to keep the tree balanced when new letters are added.

Notation 

• a stick, with a letter and a thread at both ends, or
• nothing

This leads to the following textual representation of a balance:

• if it is a stick: the number of the letter on it, followed by what is attached to its left thread, followed by what is attached to its right thread.

• if it is a loose thread: the number 0.

Within a line, numbers are separated with at least one space. The textual representation of a tree may run over several lines. Each line contains at least one number.

Input 

• a description of a balance (see notation above)

• on a separate line the number b of letters to be added, then, beginning on the next line

• b numbers, representing a letter l to be added ( ).

Within a line, the numbers of the letters to insert are separated by at least one space. The numbers of the letters may run over several lines. Each line contains at least one number.

Output 

Sample Input 

2
3 2 0 0 
5 0 0
4
1 6 7 
9
400 250 0 0 0
2
511 100

Sample Output 

3
0